SPHINCS+

A deep dive into the sig scheme in @roasbeef's proposal for post-quantum bitcoin sigs

Presidio Bitcoin, a Bitcoin-only co-working space in San Francisco, held a summit last week about Quantum Bitcoin. @roasbeef, lead maintainer of `btcd` and `lnd` and CTO of Lightning Labs, presented a proposal for adding a post-quantum signature scheme to Bitcoin, SPHINCS+. In today’s edition, Insider’s protocol-expert @niftynei breaks down the proposal.

The Quantum Problem

Most coins on chain in Bitcoin are secured with private keys. To move Bitcoins around on-chain, you prove that you have permission to spend them by creating a signature. A valid signature can only be produced by someone who possesses the correct private key.

In some sense, Bitcoin is “security by obscurity”, where the obscurity is how hard it is to guess your private key. The number of possible private keys is astronomically large. Guessing all the private keys would take more time and energy than anyone has access to in a reasonable timeframe (think hundreds of years).

However, current Bitcoin keys rely on math equations that are based on elliptic curves. Elliptic curves are a clever system to rely on for creating public and private keys, as they’re generally more secure and smaller than prime factorization (another ‘math system’ that public/private key cryptography is often based on).

Elliptic curve cryptography has a problem, however. Shor’s algorithm, invented in 1994 by Peter Shor based on Fourier Transforms, means that a quantum computer with enough qubits can quickly compute the private key of any public key.

Shor’s algorithm means we know how to break elliptic curve cryptography, the tools to do it just don’t exist yet. Whether they will exist, and when, is a topic of much debate not just in bitcoin circles, but the wider cryptographic ecosystem. The security of every private key in bitcoin depends on the tools to execute Shor’s algorithm remaining out of reach of everyone for the indefinite future.

General consensus is that at some point, bitcoin will need to transition to a post-quantum cryptosystem for public and private keys. @roasbeef’s proposal at Presidio Bitcoin last week is based on the SPHINCS+ hash-based signature scheme. Let’s dig in briefly to how it works and why it’s potentially a good fit for securing bitcoins.

Quantum secure but data heavy

SPHINCS+ is a signature construction that’s built on hashes. At its core, it relies on cryptographic hashes to construct public keys and verify signatures, rather than elegant elliptic curve equations or hiding in large number prime factorization. Hash-based crypto schemes are safe from Shor’s algorithm because they don’t use functional math systems under the hood for their one-way functions. Instead, they rely on brute force data mashing of preimages. Brute force has no mathematical relationships or short cuts that are vulnerable to quantum computer Fourier transformations, of the likes that Shor’s algorithm uses.

A downside to mashed data, aka hash functions, is that their public keys and signatures require much more data to be shared. Elliptic curves were chosen for blockchains by Satoshi himself, precisely because of how little data needed to be shared to confirm a signature or lock coins up to a public key. I like to say that Bitcoin was the killer app of elliptic curve cryptography; prior to Satoshi’s use of secp256k1 in the protocol, the majority of cryptosystems used RSA, or prime factorization, as their underlying math system. According to the SEC 2 parameters paper, a 128-bit secure RSA signature would require 3072 bits for a public key; the elliptic curve equivalent only requires 256 bits.

Using very little data is important in blockchain systems, as any data that is added to the chain must be stored and sent to every single peer on the network. Compact signatures and public keys mean that more transactions can fit into the same amount of data. Size savings is arguably the reason why Satoshi chose to use elliptic curves instead of RSA cryptography for bitcoin.

Post-quantum cryptosystems are impossibly large in comparison. SPHINCS+ systems have equivalent sized public keys to the current Bitcoin key system at 32-bytes but the signature sizes are thousands of bytes larger. A Segwit v1 Schnorr signature is 64-bytes of onchain data; comparable SPHINCS+ benchmark sigs are 3-7k bytes.

From NIST SPINCS+ parameters paper

SPHINCS+

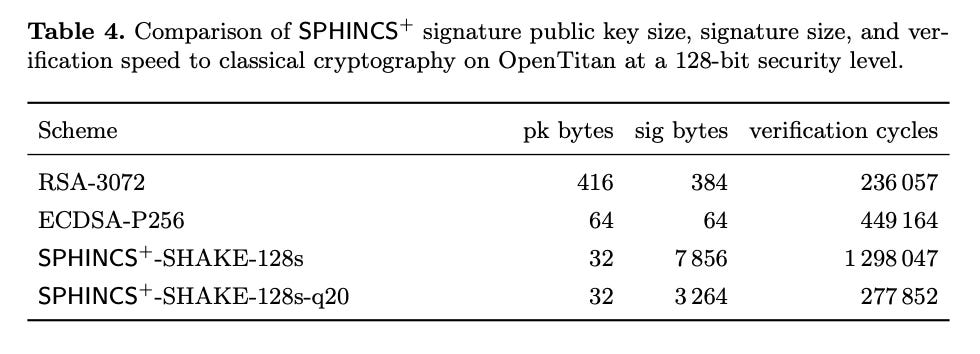
SPHINCS+ is a complex signature scheme, built using several layers of post-quantum signature ‘widgets’. When combined, SPHINCS+ produces a single quantum safe public / private keypair which can be used to sign many messages safely. Unlike XMSS (eXtended Merkle Signature Schemes), a prior post-quantum signature scheme that SPHINCS+ is an improvement over, you don’t need to remember anything about prior signatures made with the keypair for any subsequent signatures.

One SPHINCS+ “structure” produces a single pubkey that can safely sign many messages without revealing the secret key.

A SPHINCS+ 'structure’ is constructed of three different pieces:

• FORS, or “Forest of Random Subsets”. This is at the bottom of the SPHINCS+ “structure” and is where the message is used to choose a series of preimages to reveal. This set of revealed preimages becomes the base of the SPHINCS+ signature. In SPHINCS+, the message is effectively ‘signed’ using FORS. The next pieces are used to tie the FORS signature to the root public key for the SPHINCS+ superstructure, as I’m choosing to call it.

• WOTS+, or “Winternitz One Time Signatures+”. This is a post-quantum hash based signing algorithm that can sign one message securely. SPHINCS+ uses WOTS+ signatures to tie the revealed preimages in the FORS into layered-XMSS Merkle trees. The root of the layered Merkle trees is the SPHINCS+ pubkey. (The only difference between WOTS and WOTS+ is that the + variant includes a random prefix in every hash operation, which mitigates multi-target hash attacks. The ‘+’ in SPHINCS+ also means that every hash in the SPHINCS+ includes a randomly generated prefix.)

• XMSS Merkle trees. An XMSS Merkle tree has WOTS+ public keys as each of the leaves. SPHINCS+ builds huge pyramid-like structures out of layers of XMSS Merkle trees. Trees on top of trees are also commonly referred to as “hypertrees”. Each leaf of the parent tree is a WOTS+ public key. The key is used to sign the root of the tree underneath itself in the structure. This ties the trees together. How many trees and how many layers are changeable depending on the desired size of the signature for a SPHINCS+ ‘superstructure’. The smaller the signature, the more hashing will have to be done to verify and produce signatures. Each leaf at the very bottom of all the trees is a FORS. Many layers of many Merkle trees means many many many FORS at the base of the pyramid that can be used for making secure signatures with very little possibility of reuse.

Overly simplified hyper tree diagram. The PK in above would actually be the FORS signature in a SPHINCS+ situation. The `root` is the SPHINCS+ public key.

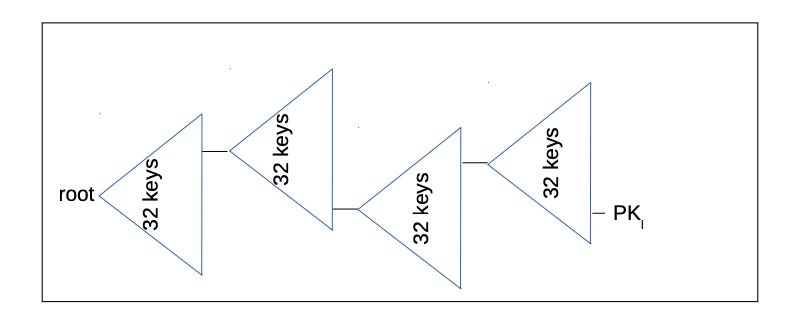
The general work of producing a SPHINCS+ public key is to generate all of the WOTS+ public keys that are at the root of the tree, and then calculate the Merkle root for that tree. The root of the top tree is the SPHINCS+ public key. The root of a Merkle tree is the same size as the hash function used to calculate the root. Typically we use SHA256 as the chosen hash function, which output 256-bits. This means that the root for such a Merkle tree is 32-bytes. This is where the SPHINCS+ public key comes from.

Creating a signature for SPHINCS+ requires using a hash of the message to randomly pick which sub-tree’s subtree the FORS signature will be connected to the SPHINCS+ ‘hypertree’ at. Once the FORS signature is created, it’s then tied into the SPHINCS+ hypertree by signing the FORS signature with the WOTS+ private key at the randomly selected sub-sub-sub-tree leaf. From there, signatures and Merkle paths are collected until you reach the root SPHINCS+ public key. All of the of WOTS+ signatures, plus the FORS signature, plus the series of Merkle paths to trace from the root SPHINCS+ pubkey to the place where the FORS signature was tied into the structure are the signature of the message. This is a lot of data, as one can imagine, and is why the signatures for SPHINCS+ are orders of magnitude greater than a simple 64-byte elliptic curve equation result and nonce value.

Diagram of data that’s included in a SPHINCS+ signature. The ‘sign’ process at right is a FORS signature; the ‘sign’ in the middle of the diagram is a WOTS+ signature.

Why SPHINCS+

SPHINCS+ is quite layered. It’s much more kludgey and relies on several different “widgets” to produce signatures: Witnernitz signatures, FORS, and XMSS subtrees.

SPHINCS+’s complexity comes from its powerful set of features. It is a strict improvement on XMSS by itself, another post-quantum signature scheme that allows for signing multiple messages. Unlike XMSS, where you must track each Merkle leaf that has already been used to sign, SPHINCS+ uses randomness generated from the message digest to deterministically select a random sub-leaf in the hypertree.

In Bitcoin, you’re ideally rotating public keys for every transaction, which means generating a new SPHINCS+ superstructure for *every* bitcoin pubkey that you use.

Initially I was confused about why you would want such powerful re-signing capability into what’s (ideally) a single use public key.

Jonas Nick of Blockstream Research pointed out that you would want to be able to re-sign a transaction for fee bumps or if a transaction was lost for some reason; Laolu, aka roasbeef, highlighted that off-chain protocols like Lightning require repeated signing of transactions for tracking private state transitions.

You likely wouldn’t need enormous resigning capability for Bitcoin, which would allow you to build smaller SPHINCS+ super structures under each pubkey. Smaller super structures would mean less data required for each signature, as the Merkle tree path data would be reduced. It also means that there’s less signatures that you can make before beginning to degrade the security. Unlike elliptic curve equations where nonce reuse immediately leaks the private key, over usage of a SPHINCS+ pubkey for signatures merely begins to degrade the security downwards from 128-bits as the FORS at the bottom get partially reused.

After digging into it, I have to say I’m quite a fan of roasbeef’s proposal to use SPHINCS+ as a post-quantum signature scheme. There’s still lots of design work to be done for exact parameters. I expect a draft BIP proposal, which he has indicated is in the works, will help fill in some of the gaps around depth of the super-structure and number of signatures that can safely be made from a single keypair.

Also worth pointing out, as mentioned in roasbeef’s presentation, SPHINCS+ doesn’t allow for seed/child derivation paths. This means that BIP32 hierarchical wallets and would be effectively dead. There’s other options here, but we’d likely lose the ability to describe keys in a wallet using hierarchical derivation paths, as is the custom these days for xpubs and child wallets.

Which way Western man

Bitcoin will move to a post-quantum signature scheme. When, what construction, and with what parameters is likely to be a hot topic of conversation for the next few years.

Roasbeef’s proposal for SPHINCS+ is a compelling option, despite the level of complexity built into the multi-layer tree superstructures. All hash-based post-quantum public key proposals are quite ugly in my opinion. SPHINCS+ is ugly because it offers the most features, specifically the statelessness of repeated signings.

With a better understanding of the role each piece plays in the protocol, I have a strong appreciation for the cleverness that led to it’s very layered setup.

Roasbeef still has his work cut out for him in writing the BIP, particularly in choosing the depth of each tree and the number of sub-tree layers, as well as the size of the Winternitz signatures and the FORS parameters. There’s a tradeoff between the size of signatures and the amount of hashes that are required to produce the signature. Choosing the right balance between computation and on-chain footprint is work that still needs to be done before publishing a formal BIP proposal.

And there’s a last question that remains to be answered:

Would moving to SPHINCS+ mean that Bitcoin is now a pyramid-scheme? Hard to say definitively, but it certainly looks that way.

Credits

Thanks to Jonas Nick and Olaoluwa Osuntokun for their help in explaining the reuse cases and tuning parameters for SPHINCS+.

Further Reading

Want to dig in further? Here’s some excellent resources that we relied on for writing this article

• Laolu’s original presentation given at the Quantum Summit at Presidio Bitcoin on July 17.

• Sphere10’s Winternitz signature explainer unlocked the basics of post quantum signatures for me.

• A deep dive blogpost by software developer Ethan Rahn. Includes great diagrams and covers some of the history of post-quantum signature development.

• Incredibly in-depth presentation on SPHINCS+ by John Kelsey of NIST. The best detailed explainer I’ve seen, but definitely in the weeds.